ZEEMAN (EFFET)

ZEEMAN (EFFET)

En 1896, le physicien néerlandais Pieter Zeeman a découvert que, lorsqu’un spectre atomique est émis par une lampe soumise à un champ magnétique suffisamment élevé, chaque raie spectrale se divise en plusieurs composantes polarisées linéairement ou circulairement. Ce phénomène s’est révélé par la suite d’une extrême généralité. On peut aujourd’hui définir l’effet Zeeman comme «l’action d’un champ magnétique sur les niveaux quantiques d’un système submicroscopique S (atome, ion, molécule, noyau atomique, défaut ou impureté dans un cristal...) et, par voie de conséquence, sur les radiations électromagnétiques en interaction avec S».

La figure 1 a représente l’énergie E des niveaux quantiques d’un système S en fonction du champ magnétique B. Pour B = 0, on supposera que S possède trois niveaux 見, 廓, 塚. La transition de S entre les niveaux 見 et 廓 s’accompagne de l’absorption ou de l’émission (fig. 1 b) de la radiation de fréquence:

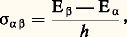où h est la constante de Planck. Étant donné deux niveaux de S, il n’y a pas toujours possibilité de transition radiative entre ces niveaux: on a supposé ainsi que la transition entre 見 et 塚 est interdite par une règle de sélection . Les radiations 靖見廓 et 靖廓塚 émises ou absorbées lors des transitions permises sont en général non polarisées, mais elles peuvent aussi être polarisées (cas de nombreuses transitions en optique cristalline).

L’énergie des différents niveaux de S est fonction de B. Par suite, la fréquence des raies spectrales correspondantes dépend aussi de B (déplacement Zeeman ). En outre, certains niveaux de S, comme 塚, restent simples en présence de champ magnétique (on dit qu’ils sont non dégénérés en absence de champ), alors que 見 et 廓 se décomposent en plusieurs sous-niveaux Zeeman 見¹, 見², 見³ et 廓¹, 廓², 廓³. On dit que 見 et 廓 sont chacun triplement dégénérés en absence de champ et que l’application du champ lève leur dégénérescence. Il en résulte une décomposition des raies spectrales correspondantes. Sur la figure 1 c, relative à un champ B¹ 0, la transition 廓塚 a donné naissance à trois composantes Zeeman du fait de la décomposition triple de 廓. La transition 見廓 a donné six composantes sur les 3 憐 3 = 9 que l’on aurait pu attendre. Comme en champ nul, certaines transitions ( 見¹廓³, par exemple) sont interdites par des règles de sélection. En général, les transitions observées en champ non nul sont polarisées, la polarisation dépendant à la fois de la transition considérée et de l’orientation de la direction d’observation par rapport au champ magnétique (et éventuellement par rapport aux axes cristallographiques).

Dans ce qui précède, on a envisagé des transitions telles que 見¹廓¹, 廓²塚, ... entre deux sous-niveaux Zeeman correspondant à deux niveaux d’énergie distincts en champ nul. Mais on peut également observer des transitions telles que 見¹見² entre sous-niveaux Zeeman correspondant à un même niveau en champ nul. L’étude de ces transitions «internes» fait partie de la spectroscopie des radiofréquences (cf. MAGNÉTOCHIMIE, SPECTROSCOPIE): résonance magnétique nucléaire si le système S est un noyau atomique, résonance paramagnétique électronique si S est un centre paramagnétique, etc. Ces diverses techniques, traitées ailleurs, sont étroitement liées à l’effet Zeeman.

1. Théorie quantique

Aussitôt après la découverte de Zeeman, Lorentz en a donné une interprétation dans le cadre de la mécanique et de l’électromagnétisme classiques. La théorie de Lorentz ne rend compte que d’une partie des phénomènes observés (effet Zeeman dit normal , cf. chap. 2, Effet Zeeman linéaire ) et elle est complètement abandonnée de nos jours au profit d’une interprétation quantique parfaitement satisfaisante. En fait, les efforts déployés pour expliquer les diverses particularités de l’effet Zeeman ont joué historiquement un rôle important dans l’élaboration de la mécanique quantique actuelle.

Une étude rigoureuse de l’effet Zeeman est pratiquement impossible, sauf pour les systèmes submicroscopiques S les plus simples. Deux considérations servent de guides et permettent d’obtenir des résultats en très bon accord avec l’expérience. D’une part, les champs magnétiques réalisables sont suffisamment faibles pour que leur action puisse se traiter par la méthode des perturbations avec une précision excellente. D’autre part, de nombreuses conclusions générales, indépendantes de l’intensité du champ ち, découlent de la symétrie géométrique du problème. Le hamiltonien qui décrit le système submicroscopique S peut s’écrire:

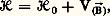où 流⁰ décrit S en absence de champ magnétique appliqué et où V⁽ size=1^ち) représente l’interaction entre S et le champ magnétique ち. Pour ち = 0, le hamiltonien 流⁰ possède souvent une symétrie suffisante pour que:

a ) ses états propres aient une dégénérescence essentielle (c’est-à-dire liée à la symétrie); c’est le cas des niveaux 見 et 廓 de la figure 1;

b ) certaines transitions entre ces états propres soient interdites par des règles de sélection (transition 見塚 de la fig. 1); ces règles de sélection sont d’autant plus strictes que la symétrie géométrique de 流⁰ est plus élevée.

Un champ magnétique uniforme ち possède la symétrie C size=1^秊h , c’est-à-dire celle d’un cylindre de révolution d’axe ち en rotation autour de cet axe (cf. CRISTAUX – cristallographie, chap. 4). Si donc ち est différent de zéro, la symétrie du hamiltonien total 流 est nécessairement inférieure ou égale à C size=1^秊h . Cette symétrie relativement faible explique le fait que les états quantiques de S en présence de champ soient non dégénérés, sauf peut-être des coïncidences accidentelles comme le croisement de niveaux qui se produit pour le champ B^c sur la figure 1 a. Cependant, la symétrie de 流 reste généralement suffisante, même en champ non nul, pour que subsistent des règles de sélection et qu’apparaissent des règles de polarisation.

Au chapitre 2, on montrera comment les principes que l’on vient d’esquisser s’appliquent à l’effet Zeeman le mieux connu, celui des atomes libres.

2. Effet Zeeman des atomes et ions libres

Généralités

Pour un atome ou un ion libre (dans la suite de l’article, on utilisera le mot «atome» pour désigner l’une ou l’autre entité), la symétrie géométrique de 流⁰ comporte, notamment, toutes les rotations autour d’axes passant par le noyau atomique O. Il en résulte qu’en champ magnétique nul chaque niveau propre Eⁱ possède un moment cinétique total づ de module bien défini 連F(F + 1), avec F = 0, 1, ... ou avec F = 1/2, 3/2, ... et une dégénérescence d’ordre 2F + 1. On prendra ici h /2 神 comme unité de moment cinétique. Les règles de sélection pour les transitions dipolaires électriques ou magnétiques (les plus intenses et les seules considérées ici) sont:

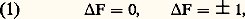les transitions entre deux niveaux de F = 0 étant interdites.

Si ち est non nul, on peut prendre sa direction comme axe des z , convention qui sera conservée dans toute la suite. La symétrie géométrique de 流 se réduit à C size=1^秊h . Le moment cinétique total des niveaux propres de 流 n’est plus défini en toute rigueur, mais la composante F^z de づ suivant l’axe Ozreste bien définie: F^z = M, avec M = 0, 梁 1, ... ou avec M = 梁 1/2, 梁 3/2, ... Les règles de sélection s’écrivent M = 0 ou 梁 1 et s’accompagnent de règles de polarisation. Pour les transitions dipolaires électriques (les plus intenses):

– Une transition M = 0 est dite transition 神. Elle est polarisée linéairement, parallèlement à Oz 轢, et n’apparaît donc pas en observation longitudinale , c’est-à-dire dans la direction de ち.

– Une transition M = + 1 en absorption (ou M = 漣 1 en émission) est dite transition 靖⁺. Elle est généralement polarisée elliptiquement et prend des polarisations simples pour deux directions particulières d’observation: pour l’observation transversale (si l’on regarde perpendiculairement à la direction de ち), elle est polarisée linéairement, perpendiculairement à Oz 轢; en observation longitudinale, elle est polarisée circulairement dans le sens de la rotation du courant électrique qui crée le champ ち. L’intensité des composantes 靖⁺ est deux fois plus grande en observation longitudinale qu’en observation tranversale.

– Une transition M = 漣 1 en absorption (ou M = + 1 en émission), est dite transition 靖^-. Elle présente les mêmes caractéristiques qu’une transition 靖⁺, mis à part une inversion du sens de rotation des vibrations elliptiques ou circulaires.

Dans le cas de transitions dipolaires magnétiques (beaucoup moins intenses que les précédentes), les règles de polarisation sont inchangées en observation longitudinale. En revanche, en observation transversale, ce sont les raies M = 0 qui apparaissent polarisées perpendiculairement à Ozet les raies M = 梁 1 parallèlement à Oz 轢.

Négligeant des termes en B² dont l’effet est très peu important pour les intensités de champ magnétique pratiquement réalisables, le hamiltonien V⁽ size=1^ち) d’interaction entre atome et champ d’induction peut se mettre sous la forme 漣 紐. ち, où 紐est l’opérateur moment magnétique atomique. En détaillant l’expression de 紐 轢, on obtient:

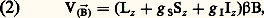où 廓, le magnéton de Bohr , est égal à eh /4 神m , d’où 廓/h = 14,0 GHz 練 ^-1 et où L^z , S^z , et I^z sont respectivement les composantes suivant Ozdes opérateurs に, moment cinétique électronique total, ひ, moment cinétique total de spin électronique, et と, moment cinétique nucléaire. Les coefficients g ^S et g ^I sont sans dimension. le coefficient g ^S égal est à 2,002 32, valeur déterminée théoriquement par l’électrodynamique quantique et parfaitement confirmée par l’expérience. Le coefficient g ^I, appelé facteur de Landé nucléaire , dépend du noyau de l’atome; il peut être positif ou négatif, mais il reste toujours de l’ordre de 10^-3 ou de 10^-4, de sorte que, dans l’expression (2), le terme en g ^II^z est généralement très faible par rapport aux deux autres; il est complétement absent pour les isotopes dépourvus de spin nucléaire. On considérera ci-dessous un tel isotope sans spin nucléaire. On désigne alors traditionnellement par ど l’opérateur moment cinétique total:

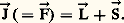Atome sans spin nucléaire. Effet Zeeman linéaire

Quand ち est assez faible pour que les décompositions Zeeman de chaque niveau soient très petites devant l’écart entre les niveaux en champ nul, il suffit d’utiliser la théorie des perturbations à l’ordre le plus bas. Un niveau de champ nul d’énergie E⁰, de moment cinétique total 連J(J + 1), se décompose en 2J + 1 sous-niveaux Zeeman équidistants, caractérisés chacun par une valeur différente de J^z = M^J, avec M^J = 漣 J, 漣 J + 1, ..., J. Les énergies de ces sous-niveaux sont:

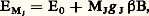où le facteur de Landé g ^J est un coefficient sans dimension, caractéristique du niveau atomique considéré. Pour une transition entre un niveau (E⁰, J) et un niveau (E ⁰, J ), la position de l’ensemble des composantes Zeeman de la raie émise ou absorbée se calcule en fonction de deux paramètres seulement, les facteurs de Landé g ^J et g ^J des deux niveaux en question (voir sur la figure 2 c l’exemple des transitions entre un niveau de J = 1/2 et des niveaux J = 1/2 et J = 3/2). De plus, l’intensité relative des différentes composantes Zeeman d’une transition (E⁰, J)(E ⁰, J ) peut être calculée une fois pour toutes, indépendamment de la nature de l’atome en question.

Le tableau indique les intensités en observation longitudinale pour les composantes 靖⁺ et 靖^- et les intensités en observation transversale pour les composantes 神. En observation transversale, il convient de diviser par 2 les intensités indiquées pour les composantes 靖. On peut vérifier, à partir du tableau, que, pour une transition (JJ ) donnée, la somme I⁺ des intensités des composantes 靖⁺ est égale à la somme I size=1^神 des intensités des composantes 神 et à la somme I^- des intensités des composantes 靖^-. Il en résulte que l’émission totale, sommée sur l’ensemble des composantes Zeeman d’une raie, est isotrope. Dans la direction du champ magnétique, on a une intensité I⁺ + I^- et, dans une direction transverse, on a une intensité égale à I size=1^神 + (I⁺ + I^-)/2. Sur la figure 2 c sont indiquées les polarisations des composantes Zeeman et leurs intensités relatives, calculées d’après le tableau.

L’effet Zeeman est un outil très utile pour l’interprétation des spectres atomiques. En observant le nombre, la polarisation et l’intensité des composantes Zeeman d’une raie spectrale, on peut déduire, d’après ce qui précède, les nombres quantiques J et J des deux niveaux en jeu dans cette transition, ce qui facilite la classification des raies, puis celle des niveaux atomiques. En outre, en mesurant la position des composantes Zeeman dans un champ d’intensité B connue, on obtient les facteurs de Landé g ^J et g ^J que l’on peut comparer à des valeurs théoriques calculées à partir du hamiltonien «perturbateur» V⁽ size=1^ち) de l’équation (2) et des fonctions d’onde décrivant les états propres de l’atome en champ nul. Ce calcul est plus ou moins compliqué suivant les cas et suivant la précision requise. On se bornera à indiquer quelques résultats simples et importants. Pour de nombreux atomes, l’approximation du couplage L-S ^{[cf. ATOME]} est bonne, c’est-à-dire que chaque niveau est caractérisé non seulement par E⁰ et J, mais par des nombres quantiques L de moment cinétique orbital et S de spin total. Le facteur de Landé est alors donné par la formule:

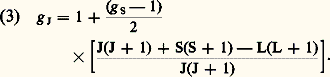Cette formule s’applique en particulier aux atomes à un électron optique (c’est-à-dire ayant un seul électron en dehors des couches saturées). Elle s’applique aussi à de nombreux atomes à plusieurs électrons optiques (notamment parmi les atomes légers). Pour certains atomes lourds, il est préférable d’utiliser l’approximation du couplage j-j (cf. ATOME, chap. 2). Avec deux électrons optiques en couplage j-j , chaque niveau est caractérisé non seulement par E⁰ et J, mais également par les nombres quantiques j ¹ et j ² de moment cinétique total du premier et du deuxième électron optique. Le facteur de Landé s’écrit alors:

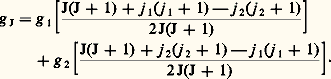Le facteur de Landé g ¹ (ou g ²) du premier (ou du deuxième) électron optique supposé seul se calcule par la formule (3). Pour certains atomes lourds, le couplage n’est ni L-S pur ni j-j pur mais intermédiaire , et le calcul des facteurs de Landé est plus compliqué.

Signalons enfin le cas particulier des niveaux de singulet en couplage L-S pur. Il s’agit des niveaux pour lesquels S = 0. On a alors L = J, et la formule (3) donne g ^J = 1. Pour une transition optique entre deux niveaux de singulet, les intervalles énergétiques entre sous-niveaux Zeeman sont les mêmes dans les deux niveaux (la figure 6 de l’article ATOME donne un exemple d’une telle transition avec J = 1 et J = 2). Il en résulte que toutes les composantes 神 ont la même fréquence:

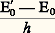et que toutes les composantes 靖 size=1^梁 ont les mêmes fréquences:

c’est ce que l’on appelle l’effet Zeeman normal , celui que permettait d’expliquer la théorie classique de Lorentz. L’effet normal est en fait beaucoup moins répandu que l’effet dit anormal , celui de toutes les raies autres que les transitions singulet-singulet, en couplage L-S pur.

Atome sans spin nucléaire. Effet Paschen-Back

Quand le champ magnétique devient trop intense pour que l’on puisse considérer 廓B comme très petit devant l’écart entre les niveaux en champ nul, la théorie des perturbations doit être poussée à un ordre supérieur. Il en résulte que:

– Les positions des composantes Zeeman ne dépendent pas linéairement de B; on peut les représenter par des développements en série où l’on ne néglige plus les termes en B², B³, etc.

– Les intensités des composantes Zeeman ne restent pas égales aux valeurs constantes données dans le tableau. On peut les représenter par des développements en série où l’on ne néglige plus les termes en B, B², etc.

Ces écarts aux lois simples de l’effet Zeeman linéaire portent le nom d’effet Paschen-Back . Très souvent, il suffit de traiter le problème de la perturbation magnétique à l’intérieur d’un multiplet de structure fine, c’est-à-dire, en couplage L-S pur, pour l’ensemble des niveaux provenant de l’effet du couplage spin-orbite sur un terme spectral de L et de S donnés. On est alors amené à diagonaliser le hamiltonien: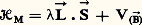

sur la base des (2S + 1)(2L + 1) fonctions correspondant à un S et à un L donnés. La quantité V⁽ size=1^ち) est la perturbation magnétique explicitée par l’équation (2), に 練 ひ le couplage spin-orbite, la constante de couplage spin-orbite du multiplet considéré. La figure 2 a donne les résultats de ce calcul pour les niveaux ²P^1/2 et ²P^3/2 d’un atome alcalin sans spin nucléaire. En champ faible, les deux niveaux ²P^1/2 et ²P^3/2 (séparés par l’écart 3/2) sont décomposés respectivement en deux et quatre sous-niveaux avec pour facteurs de Landé g ^1/2 = (4 漣 g ^s )/3 et g ^3/2 = (2 + g ^s )/3 (cf. formule 3, supra ). En champ intermédiaire, les quatre niveaux M^J = 1/2 ou M^J = 漣 1/2 ont des énergies qui ne varient plus linéairement en fonction de B, et le moment cinétique total J n’est plus un bon nombre quantique , tandis que sa projection M^J sur Ozconserve une valeur bien définie. En champ très fort, les divers sous-niveaux Zeeman correspondent à des valeurs bien définies des projections M^L et M^S de に et de ひ sur Oz(et, par suite, de M^J = M^L + M^S). L’énergie varie à nouveau linéairement en fonction de B (découplage Paschen-Back total ).

Soit maintenant une transition optique ²S^1/22P^1/2, ²P^3/2 pour laquelle l’état fondamental ²S^1/2, ayant un moment orbital L nul, ne donne pas lieu à l’effet Paschen-Back (l’énergie des sous-niveaux Zeeman de ²S^1/2 varie linéairement avec B jusqu’à des champs très intenses). La figure 2 b indique la variation d’intensité des différentes composantes Zeeman en fonction de B, et les figures 2 c, 2 d et 2 e schématisent les effets Zeeman observés pour trois valeurs de B.

Généralement, les phénomènes sont un peu plus compliqués que ceux décrits par les figures 2 b à 2 e, car les deux niveaux en cause possèdent usuellement un moment orbital に non nul, de sorte qu’ils donnent lieu tous les deux à des phénomènes d’effet Paschen-Back comparables à ceux de la figure 2 a. Néanmoins, les propriétés suivantes sont générales. Les règles de sélection en champ très fort sont M^S = 0, M^L = 0 (transition 神) ou M^L = 梁 1 (transition 靖 size=1^梁).

Les positions des raies composantes en champ très fort varient linéairement avec B. Elles se regroupent en trois paquets qui formeraient un triplet Zeeman normal si l’on «oubliait» que chacun est formé de plusieurs composantes. En champ intermédiaire, les positions des raies composantes varient de façon non linéaire avec B, leurs intensités dépendent de B et la seule règle de sélection qui subsiste est M^J = 0 (transition 神), M^J = 梁 1 (transition 靖 size=1^梁).

On n’envisagera pas l’effet Paschen-Back dans le cas d’un couplage j-j ou intermédiaire.

Influence du spin nucléaire

Soit maintenant un isotope de spin nucléaire non nul (cf. chap. 2, Généralités ). On est amené à distinguer quatre domaines de champ magnétique.

En champ très faible, les moments cinétiques électroniques ど et nucléaire と sont couplés pour donner une résultante づ. L’effet Zeeman est linéaire, chaque sous-niveau hyperfin F se décomposant en 2F + 1 sous-niveaux |F, M^F 礪, équidistants, d’écart g ^F 廓B, avec:

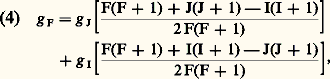expression dans laquelle g ^J désigne le facteur de Landé qu’aurait le niveau considéré en absence de spin nucléaire. Le deuxième terme de la formule (4) est beaucoup plus petit que le premier et peut, en général, être négligé. Les règles de sélection et de polarisation sont celles que donnent l’équation (1) et les paragraphes suivants. Les intensités relatives des composantes Zeeman d’une raie hyperfine donnée s’obtiennent par les formules du tableau en y remplaçant J par F, J par F et M^J par M^F.

En champ magnétique moyen, les moments cinétiques と et ど se découplent, ce qui cause une variation des probabilités de transition et une non-linéarité de la position des composantes en fonction de B (effet Back-Goudsmit ). Ce que l’on a dit à propos de l’effet Paschen-Back se transpose ici en remplaçant L par J, S par I, J par F, M^L par M^J, M^S par M^I, M^J par M^F, g ^L = 1 par g ^J, g ^S par g ^I, g ^J par g ^F et le couplage spin-orbite par le couplage hyperfin. Comme le couplage hyperfin est généralement bien plus faible que l’interaction spin-orbite, l’effet Back-Goudsmit s’observe dans des champs B plus faibles que l’effet Paschen-Back.

En champ magnétique plus élevé, le découplage と- ど est total; les niveaux sont caractérisés par les nombres quantiques I, J, M^I et M^J; leurs énergies varient à nouveau linéairement avec B et les règles de sélection sont d’une part M^I = 0, d’autre part M^J = 0 pour les composantes 神 et 梁 1 pour les composantes 靖 size=1^梁. On observe alors un spectre Zeeman analogue à celui que donnerait le même atome dépourvu de spin nucléaire, mis à part que chacune des composantes Zeeman, au lieu d’être simple, est formée de 2I + 1 «sous-composantes» équidistantes, d’intensités égales et correspondant chacune à une valeur possible de M^I. Cette particularité a permis la détermination expérimentale du spin nucléaire I d’un certain nombre d’isotopes.

En champ magnétique fort, に et ひ se découplent. C’est l’effet Paschen-Back que l’on a déjà décrit.

3. Effet Zeeman des molécules libres

Dans un champ magnétique suffisamment faible, les molécules subissent un effet Zeeman linéaire semblable à celui d’un atome: un niveau de moment cinétique total 連F(F + 1) se décompose en 2F + 1 sousniveaux équidistants, avec un écart g ^F 廓B entre sous-niveaux consécutifs. Les règles de sélection et de polarisation restent les mêmes que pour un atome libre. Le moment magnétique 漣 g ^F 廓 づ d’un niveau moléculaire résulte de trois contributions:

– les moments électroniques (orbitaux et de spin);

– le moment dû à la rotation d’ensemble de la molécule;

– les moments de spin nucléaire.

La première contribution est de l’ordre du magnéton de Bohr 廓, les deux autres de l’ordre du magnéton nucléaire qui est 1 836 fois plus petit. On peut donc classer les niveaux moléculaires en deux catégories: ceux pour lesquels la première contribution s’annule exactement (ce sont les niveaux ¹ et ils ont une décomposition Zeeman particulièrement faible); ceux pour lesquels la première contribution n’est pas nulle (on peut alors négliger les deux autres en bonne première approximation).

L’étude expérimentale de l’effet Zeeman est difficile pour les spectres optiques des molécules. En effet, pour les niveaux ¹ , les champs magnétiques les plus intenses que l’on sache produire ne donnent pas une décomposition comparable à la largeur Doppler des raies. Dans d’autres cas, les niveaux supérieur et inférieur d’une transition donnée ont pratiquement la même structure Zeeman et, par suite de règles de sélection, la décomposition de la raie optique est trop faible pour être détectée, bien que les deux niveaux en jeu aient une structure importante. Lorsque la décomposition Zeeman est observable optiquement, elle ne l’est souvent que pour les raies de nombres rotationnels les plus faibles (donc pour de faibles valeurs de F, ou de J en négligeant l’influence des spins nucléaires). Pour des valeurs élevées de J, le nombre de composantes est trop grand et elles sont à nouveau trop serrées pour être observées. Enfin, pour certains niveaux, le spin ひ se trouve découplé du reste du moment cinétique même dans des champs magnétiques faibles, et l’on observe l’équivalent moléculaire de l’effet Paschen-Back sans avoir pu observer l’effet Zeeman linéaire.

L’étude théorique de l’effet Zeeman moléculaire est plus compliquée que pour les atomes, mais elle est néanmoins assez avancée pour expliquer convenablement les quelques résultats obtenus par spectroscopie optique et surtout les résultats, plus nombreux et très intéressants, acquis par les méthodes de la spectroscopie des radio-fréquences, méthodes qui sont bien adaptées à l’étude expérimentale de l’effet Zeeman moléculaire (cf. SPECTROSCOPIE – Spectroscopie des radiofréquences).

4. Effets magnéto-optiques de la matière condensée

Niveaux de Landau des solides

Dans les liquides, les substances vitreuses et les cristaux, les atomes, molécules ou ions constituants sont très voisins les uns des autres (quelques dixièmes de nanomètre) et ils interagissent donc très fortement. Il en résulte que les spectres observés sont généralement très différents de ceux des atomes ou des molécules libres.

Dans la plupart des cas, on doit considérer que les électrons optiques d’un cristal ne sont pas liés à un noyau particulier, mais qu’ils appartiennent en bloc à l’ensemble de l’échantillon, se répartissant en bandes d’énergie, dont la bande de valence, la dernière à être normalement peuplée, et la bande de conduction, la première à être normalement vide (cf. physique des SOLIDES). Dans chaque bande existe un quasicontinuum d’états quantiques. Landau a montré que, sous l’effet d’un champ magnétique B, ce quasi-continuum se condense en sous-bandes (niveaux de Landau ) séparées par l’écart énergétique E^c = h Be /2 神m , où m est la masse effective des électrons de la bande considérée. On observe, d’une part des transitions entre deux niveaux de Landau de la même bande (résonance cyclotron en ondes centimétriques ou infrarouges lointaines) et, d’autre part, des transitions entre un niveau de Landau appartenant à la bande de valence et un niveau de Landau appartenant à la bande de conduction. C’est le phénomène de magnéto-absorption , observé dans le proche infrarouge pour les semiconducteurs, et qui pourrait être observé dans l’ultraviolet pour les isolants. Le front du côté des grandes longueurs d’onde de la bande d’absorption fondamentale, qui a une forme douce en absence de champ magnétique, présente, quand B est non nul, des accidents dont la position dépend de B d’une façon un peu analogue à celle des composantes Zeeman des spectres atomiques. L’extrapolation pour B = 0 de la position de ces composantes permet une détermination précise de la distance énergétique entre bande de valence et bande de conduction.

Effet Zeeman des centres localisés

On rencontre des cas où les électrons optiques, bien que perturbés par l’entourage cristallin, sont liés essentiellement à un centre donné (par exemple, centres colorés dus à des impuretés ou à des défauts de réseau, cristal pur renfermant des ions de terre rare, etc.). Les spectres sont alors assez semblables à ceux des atomes libres, les raies d’émission ou d’absorption étant simplement plus ou moins déplacées et élargies par interaction avec l’entourage. Quand l’élargissement est suffisamment faible, l’effet Zeeman présente des caractères très analogues aux caractères étudiés au chapitre 2. Il faut tenir compte, toutefois, d’une plus faible symétrie du problème non perturbé (en l’absence de ち) et de complications dues à l’orientation de ち par rapport aux axes cristallographiques. Un exemple bien connu d’un tel effet Zeeman de caractère «presque atomique» est celui des raies rouges du rubis, Al²³ dopé au Cr⁺⁺⁺.

Des effets Zeeman résolus se rencontrent également dans les spectres d’entités à comportement «individuel», bien que non localisées, comme l’exciton (ensemble électron-trou se déplaçant de conserve dans un cristal) ou le polaron (électron se déplaçant dans un cristal accompagné d’un «nuage de polarisation »).

Quand les raies dues à un centre localisé sont trop élargies pour que l’on puisse en séparer les composantes Zeeman par les champs les plus intenses que l’on sache produire, l’effet Zeeman prend la forme d’un dichroïsme magnétique en absorption, d’une polarisation magnétique en émission. Soit, par exemple, une observation longitudinale dans une expérience d’absorption. Dans le cas simple de la figure 3 a, les deux composantes Zeeman 靖 d’une raie large (ou bande) sont déplacées l’une par rapport à l’autre d’une quantité 2 g 廓B, très inférieure à la largeur de la bande. L’effet Zeeman n’est donc pas résolu, mais on observe un dichroïsme circulaire magnétique de la bande, c’est-à-dire que son flanc du côté des grandes longueurs d’onde absorbe, dans l’exemple choisi, préférentiellement la lumière 靖^- et son flanc du côté des courtes longueurs d’onde absorbe préférentiellement la lumière 靖⁺ (fig. 3 b). À ce dichroïsme circulaire magnétique dû au déplacement des composantes Zeeman peuvent s’ajouter deux autres contributions: l’une est liée aux variations des populations des sous-niveaux Zeeman du fondamental sous l’effet du facteur de Boltzmann (contribution paramagnétique , surtout importante aux très basses températures, donnant un dichroïsme circulaire magnétique de forme semblable à la bande d’absorption et non plus à sa dérivée); l’autre est due aux variations des probabilités de transition en fonction du champ magnétique par mélange entre fonctions d’onde de niveaux électroniques différents (effet Paschen-Back).

Effet Faraday

Le premier phénomène magnéto-optique connu a été l’effet Faraday ou Polarisation rotatoire magnétique (1845). Une substance quelconque, placée dans un champ magnétique ち et traversée par un faisceau lumineux linéairement polarisé, se propageant parallèlement à ち, produit une rotation 見 du plan de polarisation telle que 見 = 福l B, expression où l est l’épaisseur traversée et 福 la constante de Verdet de la substance, qui dépend en particulier de la température et de la longueur d’onde lumineuse (cf. CRISTAUX – Optique cristalline, chap. 3). L’effet Faraday résulte d’une biréfringence circulaire induite par le champ magnétique. Les indices de réfraction 益⁺ et 益^- pour les lumières circulaires 靖⁺ et 靖^-, égaux en absence de champ magnétique, prennent une valeur légèrement différente en présence de champ. Si les rotations sont exprimées en radians, on obtient:

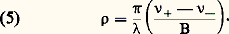L’effet Faraday est intimement lié aux phénomènes magnéto-optiques précédents. En effet, l’indice de réfraction complexe d’une substance absorbante est de la forme n = 益 漣 j 﨑, où la partie réelle 益 est l’indice de réfraction proprement dit et la partie imaginaire 﨑 l’indice d’extinction (lié au coefficient d’absorption k par k = 4 神﨑/). Les indices 益 et 﨑 dépendent tous les deux de la fréquence 靖 des ondes lumineuses et sont reliés par des formules mathématiques (transformations de Kramers-Krönig ) qui permettent de connaître la fonction 益( 靖) à partir de 﨑( 靖) et vice versa. Il en résulte qu’à chaque bande d’absorption, accident de 﨑( 靖), correspond une anomalie de dispersion, accident de 益( 靖). La figure 3 c montre les anomalies de dispersion liées respectivement aux deux composantes Zeeman de la bande d’absorption de la figure 3 a. La différence 益⁺ 漣 益^-, portée sur la figure 3 d, est proportionnelle, d’après la formule (5), à la constante de Verdet 福 qui caractérise l’effet Faraday.

On observe de même un phénomène de dispersion lié à l’effet Zeeman transversal: c’est l’effet Cotton-Mouton . Une substance naturellement isotrope, traversée par un faisceau lumineux se propageant perpendiculairement à la direction de ち, devient biréfringente. Soit 益ⁿ et 益 les indices de réfraction pour de la lumière polarisée linéairement parallèlement et perpendiculairement à ち. La différence 益ⁿ 漣 益 est proportionnelle à B².

Les effets Faraday et Cotton-Mouton ne sont pas limités aux substances solides et liquides. On les observe aussi dans les spectres atomique ou moléculaires des chapitres 2 et 3 (exemples: expérience de Macaluso et Corbino sur l’effet Faraday au voisinage des raies jaunes de l’atome de sodium, spectres dits de rotation magnétique en optique moléculaire).

Encyclopédie Universelle. 2012.